#651 - Rebus Puzzle Example
Below puzzle is a popular example for rebus puzzles.
Can you tell us what i am thinking by solving the below rebus ?
Feeling on top of the World
#653 - Counting Triangles in a Figure
Can you count the number of triangles in the given picture?
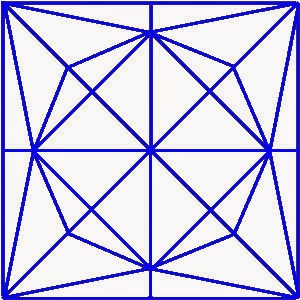
There are 92 triangles in this picture.
#654 - Can You Solve This Math Problem
A rain drop fell from one leaf to another leaf and lost 1/4th of its volume. It then fell to another leaf and lost 1/5th of the volume. It again fell on another leaf and lost 1/5th of the volume.
This process kept repeating till it fell on the last leaf losing 1/75th of its volume.
Can you calculate the total percentage of loss from the initial volume when the drop has fallen to the last leaf accurate up to two decimal places?
4%
Let us assume that the initial volume of the water drop was k.
k - (1/4) k = (3/4) k
(3/4) k - (1/5) [(3/4) k] = (3/4) k * [1 - (1/5)] = (3/4) k * (4/5) = (3/5) k
(3/75) k = (1/25) k
1/25 = 4%
Thus, the answer is four percent.
#655 - How Many Triangles Challenge
Can you find out the total number of triangles in the given figure?
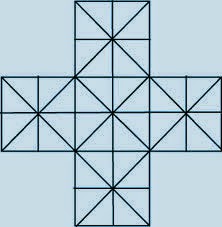
There are 60 triangles in the given figure.
#656 - Challenging Logic Problem
You order chicken wings at KFC in the boxes of 6, 9 and 20. What is the largest number of wings that you cannot obtain by buying in any combination of the boxes?
43
You know that you can purchase any number of wings that is divisible by 3 but of course it should not be 3 itself. Thus, you should just try to purchase using the combinations of 9 and 6 boxes till the number is divisible by 3. If that number is not divisible by 3, then you have to use a box with 20. If the number that remains is divisible by 3, you are game. But if it is not divisible by 3, you can use a second box of 20. The number now will necessarily be divisible by 3.
Thus the largest number of wings that cannot be bought will come after buying two boxes of 20 and leaving a remainder that is divisible by 3:
3 + 20 + 20 = 43.
#657 - Impossible Math Problem
Suppose you drive to a picnic spot at 20 mph, then how fast you must go while returning back home on the same route such that your average speed becomes 40 mph?
infinite speed
Let us denote distance with d, time to get there by T, time to get back by t and the speed while travelling back with R.
Now by applying the simple time, distance and speed formula:
d = 20T
T = d/20
d = Rt
t = d/R
As you can see, we have the equations for both T and t now. We can now finally derive and equation for the round trip.
2d = 40(T + t)
2d = 40(d/20 + d/R)
2d = 40d(1/20 + 1/R)
1 = 20(R/20R + 20/20R)
20R = 20(R+20)
R = R + 20
You can clearly see that it is a paradox as to make the average speed 40 mph, you will have to travel back at an infinite speed. The faster you return, the quicker you can make it although your faster speed will offer a lesser impact on the average speed.
If you made the return trip instantly, it would be comparable to traveling double the distance in the same time that was taken on the one way trip.
Thus to reach the average speed of 40 mph, you must return with an infinite speed.
#658 - Logic Puzzle Question
You are camping with your friends. You have a flashlight for any emergency and have brought 8 batteries along with you. Your brother calls to tell you that four of those batteries are already dead.
Your flashlight requires two working batteries to run. What is the least number of pairs you will need to test to guarantee that you can get the flashlight on ?
7
You must first divide the batteries in three groups: a group of two batteries and two groups of three batteries each. Now you have made sure that one of the group has two working batteries.
Now both the groups with three batteries can form three possible combinations and the group with two batteries has just one combination.
3 + 3 + 1 = 7.
#659 - Science Logic Puzzle
You have an empty wine bottle (too bad eh?) with a cork that has been secured at the top in a normal way. There is a metal ring inside the bottle that is suspended by a string.
How can you make the metal ring drop to the bottom if you are not allowed to touch anything - not the bottle, not the cork, not the thread and not the ring?
You just need a magnifying glass to do considering you are out in open with bright sun rays available to you. With the glass, you can burn through the string and thus making the ring drop to the bottom.
#660 - Number Squares Chess Board Teaser
In the attached figure, you can see a chessboard and two rooks placed on the chess board. What you have to find is the number of squares that do not contain the rooks.How many are there?
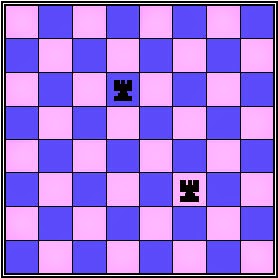
128
Lets count them one by one.
62 squares of size 1x1.
41 squares of size 2x2.
18 squares of size 3x3.
6 squares of size 4x4.
1 square of size 5x5.
62 + 41 + 18 + 6 + 1 = 128 squares.